Các Thuật Toán Sắp Xếp( So Sánh Các Thuật Toán Sắp Xếp, Thuật Toán Sắp Xếp

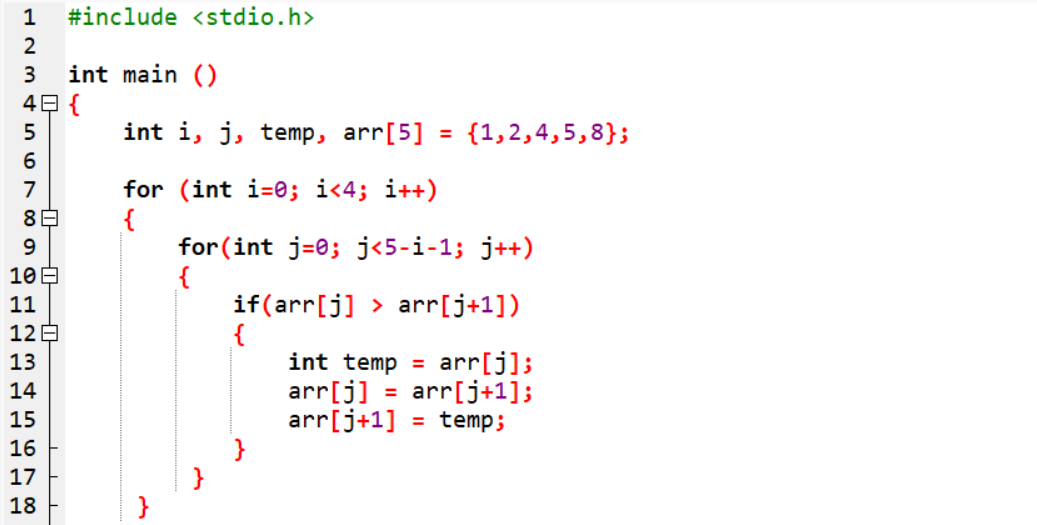
Kết quả hiển thị:

Ví dụ 2: chi tiết quá trình chuẩn bị xếp 

#include #include #define MAX 10int list = 1,8,4,6,0,3,5,2,7,9;void display()int i;printf("<");// Duyet qua tat ca phan tufor(i = 0; i list) temp = list;list = list;list = temp;swapped = true;printf(" => trao doi <%d, %d> ",list,list);else printf(" => khong can trao doi ");// neu khong can trao doi nua, tuc la// có da duoc sap xep va thoat khoi vong lap.if(!swapped) break;printf("Vong lap thu %d#: ",(i+1));display();}}main()printf("Mang du lieu dau vao: ");display();printf(" ");bubble
Sort();printf("
Mang sau khi da sap xep: ");display();Kết quả

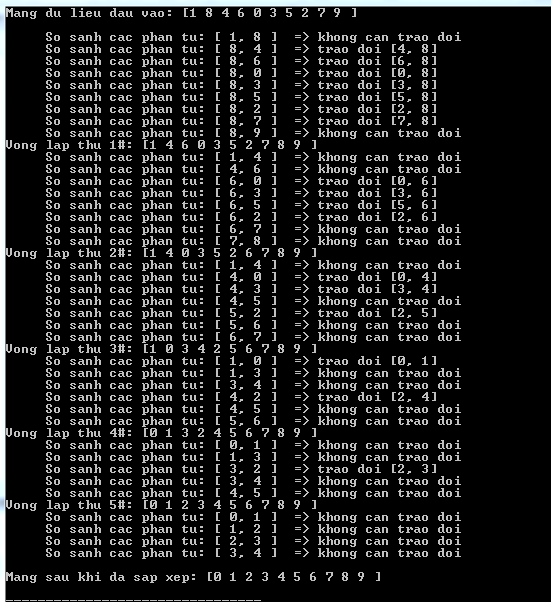
Sắp xếp chèn (Insertion Sort)

Thuật toán sắp xếp chèn là gì?

Sắp xếp chèn là 1 trong giải thuật bố trí dựa trên so sánh in-place. Ở đây, một list con luôn luôn được duy trì dưới dạng vẫn qua chuẩn bị xếp. Bố trí chèn là chèn thêm một phần tử vào list con đã qua sắp tới xếp. Thành phần được chèn vào vị trí say mê hợp làm thế nào để cho vẫn bảo vệ rằng list con này vẫn sắp theo sản phẩm tự.

Với cấu tạo dữ liệu mảng, chúng ta tưởng tượng là: mảng tất cả hai phần: một list con đang được sắp xếp và phần khác là các phần tử không tất cả thứ tự. Lời giải sắp xếp chèn sẽ thực hiện việc tìm kiếm tiếp tục qua mảng đó, cùng các thành phần không tất cả thứ tự đang được dịch chuyển và được chèn vào vị trí phù hợp trong danh sách con (của thuộc mảng đó).

Giải thuật này không thích hợp sử dụng với các tập tài liệu lớn lúc độ tinh vi trường vừa lòng xấu nhất với trường vừa lòng trung bình là Ο(n2) cùng với n là số phần tử.

Một vài phương pháp được thực hiện trong sắp xếp chèn:

Ý tưởng bài toán:

Thuật toán bố trí chèn triển khai sắp xếp hàng số theo phong cách duyệt từng bộ phận và chèn từng phần tử đó vào đúng địa chỉ trong mảng con(dãy số từ đầu đến phần tử phía trước nó) đã chuẩn bị xếp sao cho dãy số trong mảng sắp đến đã xếp đó vẫn bảo đảm an toàn tính hóa học của một hàng số tăng dần.

Sắp xếp chèn với ngôn ngữ C

Ví dụ minh họa: bố trí mảng từ bỏ thấp đến cao cần sử dụng thuật toán bố trí chèn

Kết quả hiển thị:

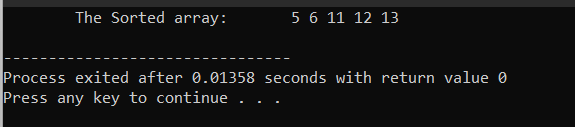
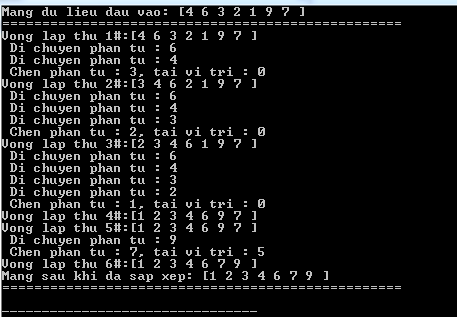
Ví dụ: cụ thể quá trình bố trí chèn

#include #include #define MAX 7int int
Array = 4,6,3,2,1,9,7;void printline(int count)int i;for(i = 0;i 0 && int
ArrayPosition-1> > value
To
Insert)int
ArrayPosition> = int
ArrayPosition-1>;hole
Position--;printf(" Di chuyen phan tu : %d " , int
ArrayPosition>);if(hole
Position != i)printf(" Chen phan tu : %d, tai vi tri : %d " , value
To
Insert,hole
Position);// chen phan tu tai vi tri chenint
ArrayPosition> = value
To
Insert;printf("Vong lap thu %d#:",i);display();}main()printf("Mang du lieu dau vao: ");display();printline(50);insertion
Sort();printf("Mang sau khoản thời gian da sap xep: ");display();printline(50);

Sắp xếp lựa chọn (Selection Sort)

Thuật toán bố trí chọn là gì?

Giải thuật sắp xếp chọn (Selection Sort) là một giải thuật solo giản. Giải mã sắp xếp này là 1 trong giải thuật dựa trên việc so sánh in-place, trong các số ấy danh sách được tạo thành hai phần, phần được bố trí (sorted list) ở bên trái và phần không được sắp xếp (unsorted list) ở bên phải. Ban đầu, phần được thu xếp là trống với phần chưa được sắp xếp là toàn cục danh sách ban đầu.

Phần tử bé dại nhất được lựa chọn từ mảng không được sắp xếp với được tráo đổi với phần bên trái tuyệt nhất và thành phần đó trở thành phần tử của mảng được sắp tới xếp. Quá trình này tiếp tục tính đến khi toàn thể từng phần tử trong mảng không được sắp xếp phần lớn được dịch chuyển sang mảng vẫn được sắp đến xếp.

Thuật toán thu xếp chọn sẽ thu xếp một mảng bằng phương pháp đi tìm bộ phận có giá chỉ trị nhỏ nhất(giả sử với thu xếp mảng tăng dần) trong khúc đoạn không được sắp xếp cùng đổi bỏ phần tử nhỏ nhất kia với bộ phận ở đầu đoạn không được sắp xếp(không cần đầu mảng). Thuật toán sẽ phân tách mảng làm 2 mảng con

Tại từng bước một lặp của thuật toán, phần tử bé dại nhất sinh sống mảng con chưa được sắp xếp vẫn được di chuyển về đoạn đã sắp xếp.

Sắp xếp lựa chọn với ngữ điệu C

Ví dụ minh họa: bố trí mảng từ thấp tới cao cùng với thuật toán sắp xếp chọn

Kết quả hiển thị

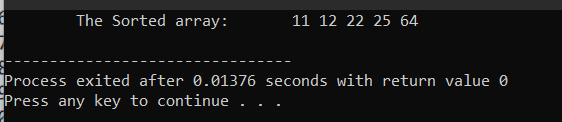
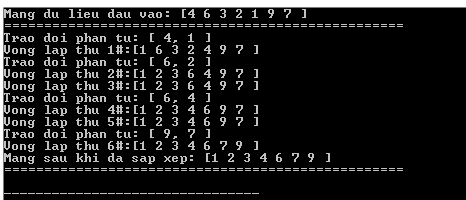
Ví dụ: cụ thể cách hoạt động của sắp xếp chọn

#include #include #define MAX 7int int
Array = 4,6,3,2,1,9,7;void printline(int count){int i;for(i = 0;i Hiển thị:

Sắp xếp trộn (Merge Sort)

Thuật toán bố trí trộn là gì?

Sắp xếp trộn (Merge Sort) là một trong những giải thuật sắp xếp dựa trên giải thuật Chia để trị (Divide và Conquer). Cùng với độ phức hợp thời gian trường thích hợp xấu nhất là Ο(n log n) thì đấy là một trong những giải thuật đáng được thân thiện nhất.

Giải thuật sắp xếp trộn phân tách mảng thành hai nửa liên tục, tới lúc còn 1 phẩn tử và sau đó kết hợp chúng lại cùng nhau thành một mảng sẽ được chuẩn bị xếp.

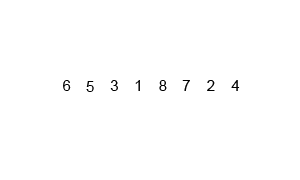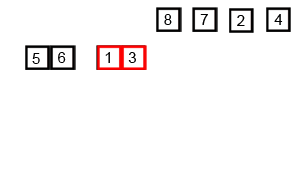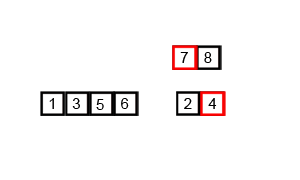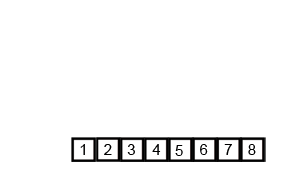
Hình hình ảnh dưới phía trên từ wikipedia sẽ hiển thị cho chính mình toàn bộ sơ đồ quy trình của thuật toán merge sort cho mảng 38, 27, 43, 3, 9, 82, 10. Nếu quan sát kỹ rộng vào sơ đồ dùng này, bạn cũng có thể thấy mảng thuở đầu được lặp lại hành động chia cho tới khi kích thước các mảng sau chia là 1.

Khi form size các mảng nhỏ là 1, các bước gộp sẽ bước đầu thực hiện gộp lại các mảng này cho tới khi xong và chỉ từ một mảng đã sắp đến xếp.

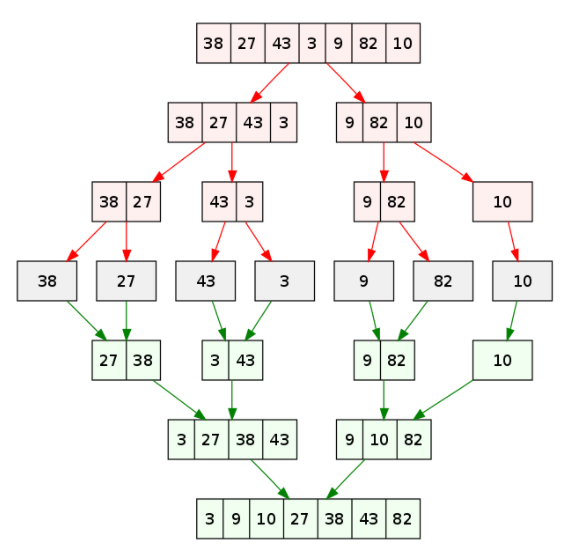
Thuật toán thu xếp trộn trong C

Ví dụ minh họa

#include #define max 10int a<10> = 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 ;int b<10>;void merging(int low, int mid, int high) int l1, l2, i;for(l1 = low, l2 = mid + 1, i = low; l1 hiện tại thị:

Sắp xếp cấp tốc (Quick Sort)

Thuật toán thu xếp nhanh là gì

Giải thuật sắp xếp nhanh (Quick Sort) là một trong giải thuật kết quả cao và dựa trên việc phân chia mảng dữa liệu thành các mảng nhỏ tuổi hơn. Giải thuật sắp xếp nhanh chia mảng thành hai phần bằng cách so sánh từng phần tử của mảng với một phần tử được chọn gọi là phần tử chốt (Pivot): một mảng bao hàm các phần tử nhỏ hơn hoặc bằng phần tử chốt với mảng còn lại bao hàm các thành phần lớn rộng hoặc bằng bộ phận chốt.

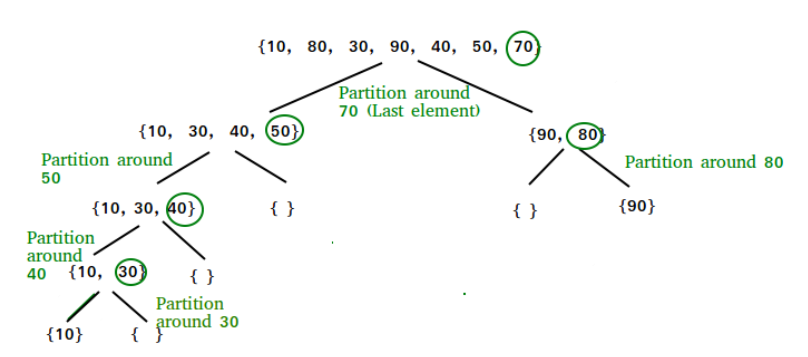
Giống như Merge sort, thuật toán sắp xếp quick sort là một trong thuật toán phân chia để trị( Divide and Conquer algorithm). Nó chọn một trong những phần tử trong mảng có tác dụng điểm tấn công dấu(pivot). Thuật toán sẽ tiến hành chia mảng thành các mảng con phụ thuộc vào pivot vẫn chọn. Bài toán lựa lựa chọn pivot tác động rất những tới vận tốc sắp xếp. Nhưng máy tính lại cần yếu biết khi nào thì nên lựa chọn theo giải pháp nào. Dưới đó là một số cách để chọn pivot hay được sử dụng:

Mấu chốt bao gồm của thuật toán quick sort là việc phân đoạn dãy số (Xem hàm partition()). Phương châm của các bước này là: cho 1 mảng và một trong những phần tử x là pivot. Đặt x vào đúng vị trí của mảng đã sắp tới xếp. Di chuyển tất cả các phần tử của mảng mà nhỏ tuổi hơn x sang bên trái vị trí của x, và di chuyển tất cả các phần tử của mảng mà lớn hơn x thanh lịch bên đề nghị vị trí của x.

Khi đó ta sẽ có 2 mảng con: mảng mặt trai của x với mảng bên bắt buộc của x. Tiếp tục quá trình với mỗi mảng con(chọn pivot, phân đoạn) tính đến khi mảng được chuẩn bị xếp.

Đặt pivot là phần tử cuối cùng của dãy số arr. Chúng ta bắt đầu từ thành phần trái độc nhất vô nhị của dãy số gồm chỉ số là left, và bộ phận phải duy nhất của dãy số gồm chỉ số là right -1(bỏ qua phần tử pivot). Chừng làm sao left pivot với arr

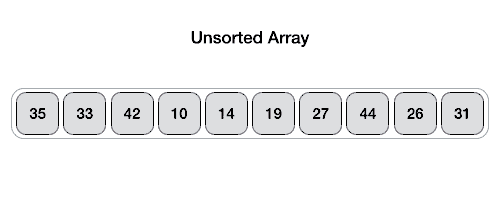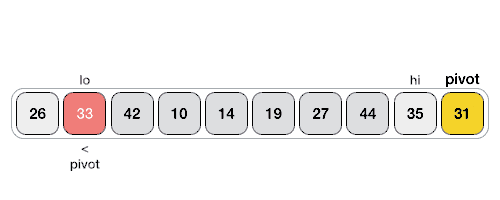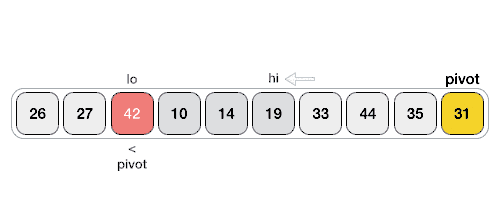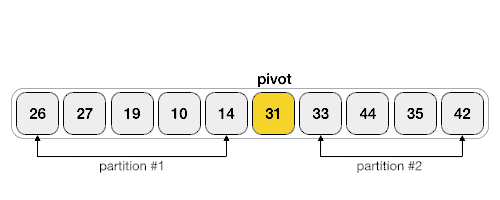
Thuật toán sắp xếp nhanh vào C

Ví dụ minh họa

#include #define MAX 7int int
Array = 4,6,3,2,1,9,7;void printline(int count)int i;for(i = 0;i 0 && int
Array<--right
Pointer> > pivot)//khong lam giif(left
Pointer >= right
Pointer)break;elseprintf(" Phan tu duoc trao doi :%d,%d ",int
ArrayPointer>,int
ArrayPointer>);swap(left
Pointer,right
Pointer);printf(" Phan tu chot duoc trao doi :%d,%d ", int
ArrayPointer>,int
Array);swap(left
Pointer,right);printf("Hien thi có sau moi lan trao doi: ");display();return left
Pointer;// tê mê sap xepvoid quick
Sort(int left, int right)if(right-left Hiển thị: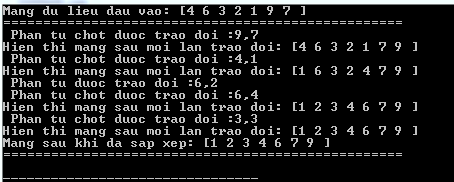

Shell Sort

Thuật toán sắp xếp Shell Sort là gì?

Shell Sort là 1 giải thuật sắp xếp mang lại hiệu quả cao dựa vào giải thuật sắp xếp chèn (Insertion Sort). Lời giải này khá kết quả với các tập dữ liệu có kích tầm trung bình bình khi nhưng mà độ phức tạp trường đúng theo xấu nhất cùng trường đúng theo trung bình là O(n), với n là số phần tử.

Giải thuật này tránh các trường hợp cần tráo đổi vị trí của hai thành phần xa nhau trong giải mã sắp xếp lựa chọn (nếu như phần tử nhỏ hơn tại đoạn bên phải khá xa so với phần tử lớn hơn mặt trái).

Đầu tiên, giải mã này sử dụng giải mã sắp xếp chọn trên các bộ phận có khoảng cách xa nhau, kế tiếp sắp xếp các phần tử có khoảng cách hẹp hơn. Khoảng cách này còn được gọi là khoảng (interval) – là số địa chỉ từ phần tử này tới bộ phận khác. Khoảng này được tính phụ thuộc các loại công thức sau

Cách Shell Sort vận động với cách làm Shell’s original sequence

Ví dụ sắp tới xết dãy a = <9, 1, 3, 7, 8, 4, 2, 6, 5> thành hàng không giảm.

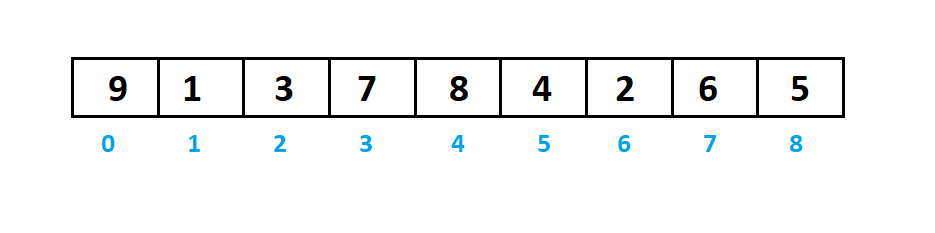
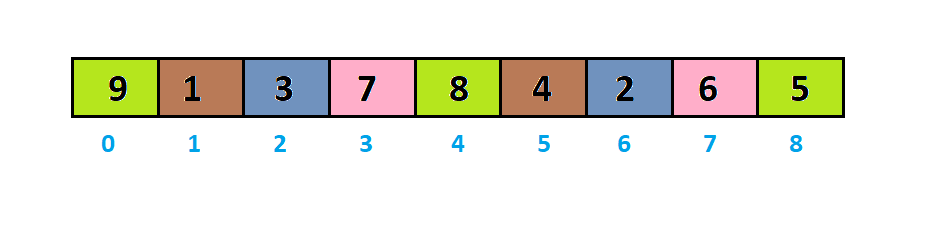
Với interval = 9/2 = 4, ta sẽ chia dãy thành các dãy bé với những số biện pháp nhau một khoảng chừng là interval: <9, 8, 5>, <1, 4>, <3, 2> và <7, 6>.

Sắp xếp đầy đủ dãy bé này theo cách sắp xếp chèn (Insertion Sort).

Sau khi sắp tới xếp những dãy bé dãy đã thành.

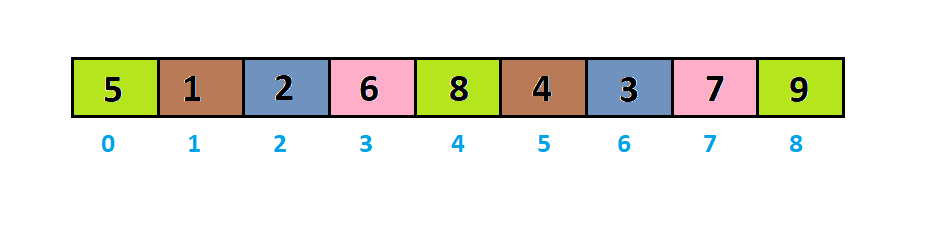
Với interval = 9/4 = 2, ta sẽ chia dãy thành các dãy bé với những số bí quyết nhau một khoảng tầm là interval: <9, 8, 5>, <1, 4>, <3, 2> và <7, 6>.

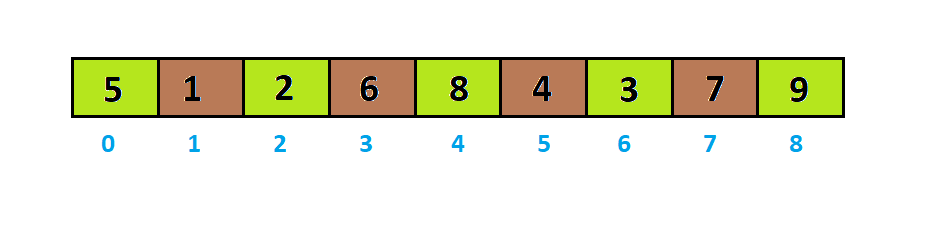
Sau khi sắp xếp các dãy bé dãy đang thành.

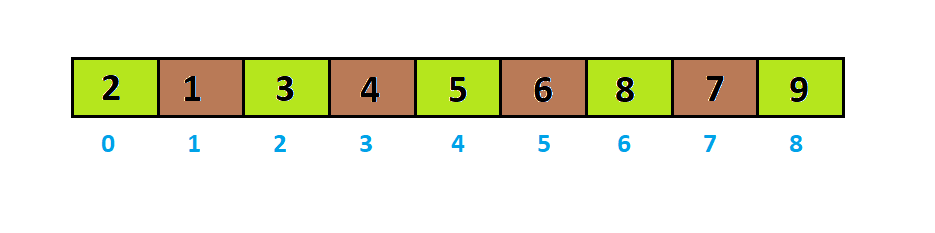
Với interval = 9/8 = 1, bây giờ interval = 1 ta áp dụng sắp xếp chèn với cả dãy a:

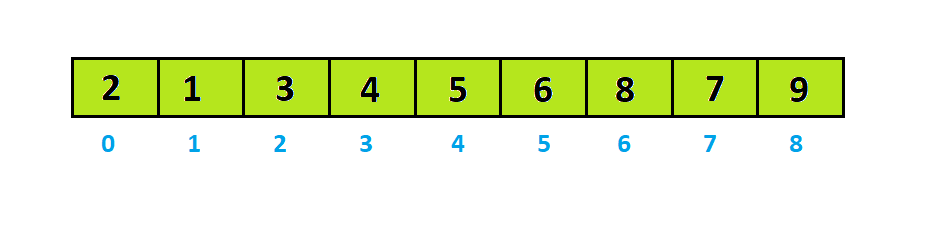
Dãy sau khi sắp xếp là:

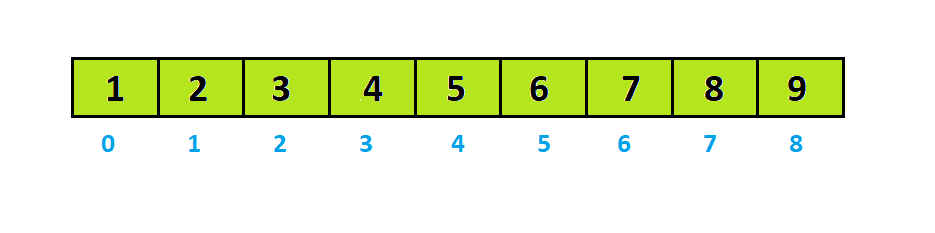
Sắp xếp Shell trong thiết kế C

Ví dụ minh họa, bài bác tập vận dụng:

#include #include #define MAX 7int int
Array = 4,6,3,2,1,9,7;void printline(int count)int i;for(i = 0;i 0) printf("Vong lap thu %d#:",i);display();for(outer = interval; outer interval -1 && int
Array>= value
To
Insert) int
Array = int
Array;inner -=interval;printf(" Di chuyen phan tu :%d ",int
Array);int
Array = value
To
Insert;printf(" Chen phan tu :%d, tai vi tri :%d ",value
To
Insert,inner);interval = (interval -1) /3;i++;int main() printf("Mang du lieu dau vao: ");display();printline(50);shell
Sort();printf("Mang ket qua: ");display();printline(50);return 1;Hiển thị: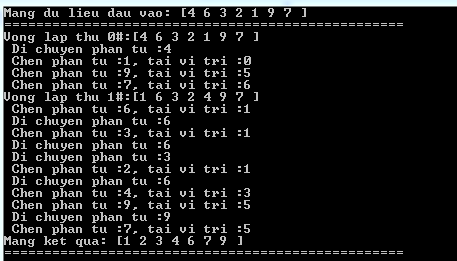

Thuật toán bố trí đếm (Counting Sort)

Thuật toán bố trí đếm là gì?

Counting sort là một thuật toán bố trí cực cấp tốc một mảng các phần tử mà mỗi phần tử là những số nguyên không âm; Hoặc là một trong danh sách những ký tự được ánh xạ về dạng số nhằm sort theo bảng chữ cái. Counting sort là một trong thuật toán sắp đến xếp các con số nguyên ko âm, không dựa vào so sánh.

Trong khi những thuật toán bố trí tối ưu sử dụng so sánh có độ phức hợp O(nlogn) thì Counting sort chỉ việc O(n) trường hợp độ dài của danh sách không quá bé dại so với bộ phận có giá chỉ trị khủng nhất.

Hình ảnh dưới phía trên cho chúng ta thấy cách hoạt động của thuật toán bố trí này.

Bước 1:

Trong những bước đầu tiên tiên, cửa hàng chúng tôi đếm số lần xuất hiện thêm của từng bộ phận trong mảng bắt buộc sắp xếp A. Công dụng được lưu giữ vào mảng C.

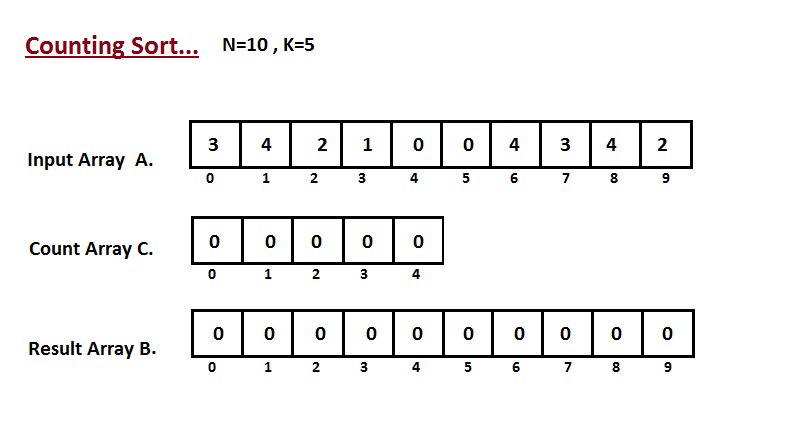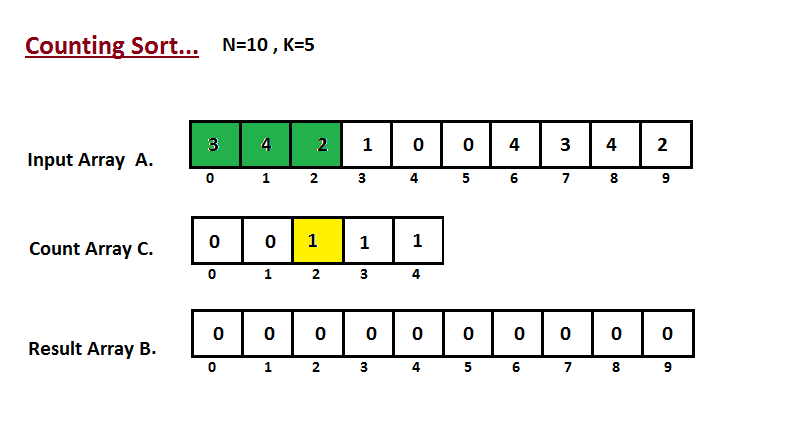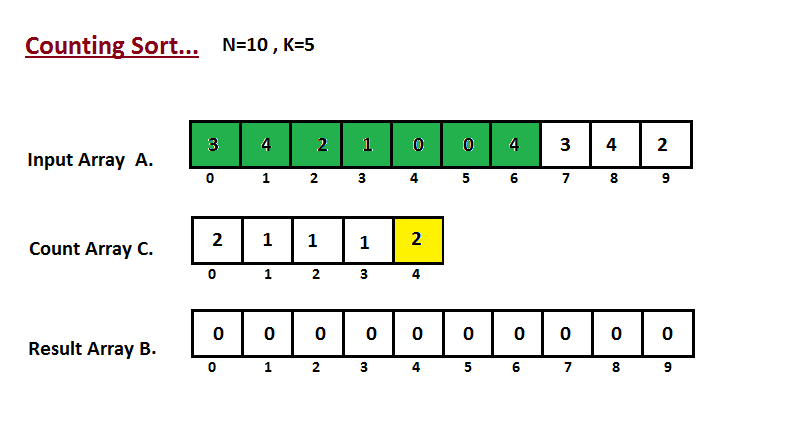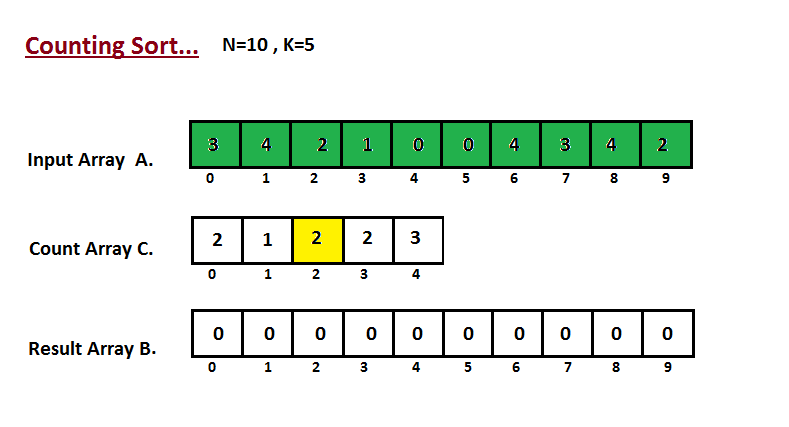
Bước 2: Ở bước này, chúng ta cần xem xét sửa đổi cực hiếm của C. C thể hiện số lượng giới hạn trên của chỉ số của phần tử i sau khi sắp tới xếp.

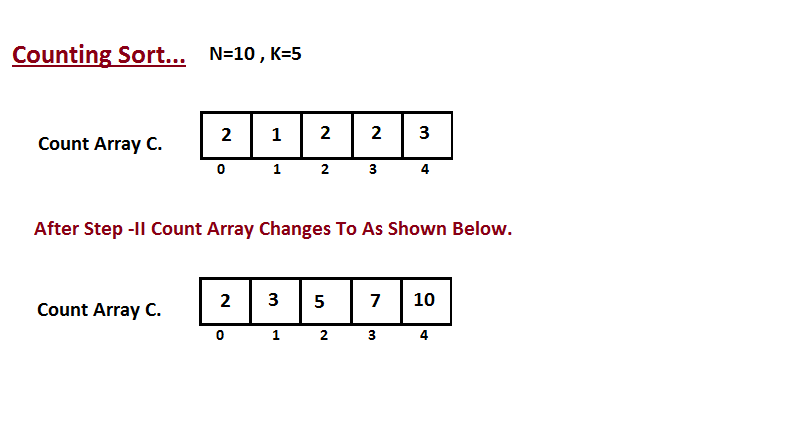
Bước 3: Duyệt qua từng thành phần của A và đặt nó vào đúng chỉ số của mảng chứa các giá trị đã chuẩn bị xếp B dựa vào C.

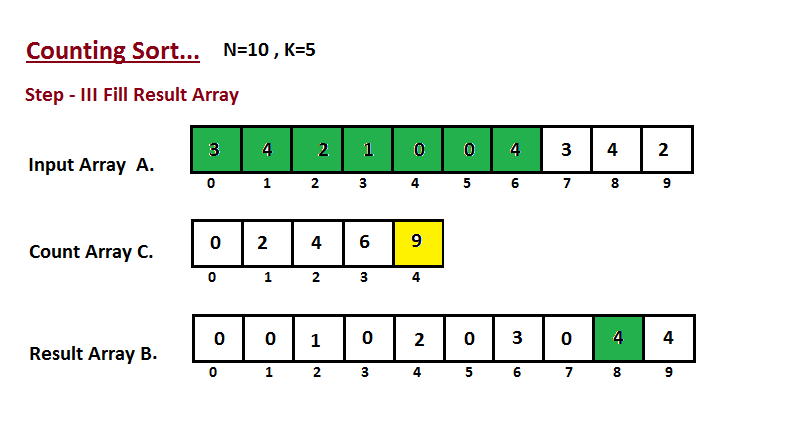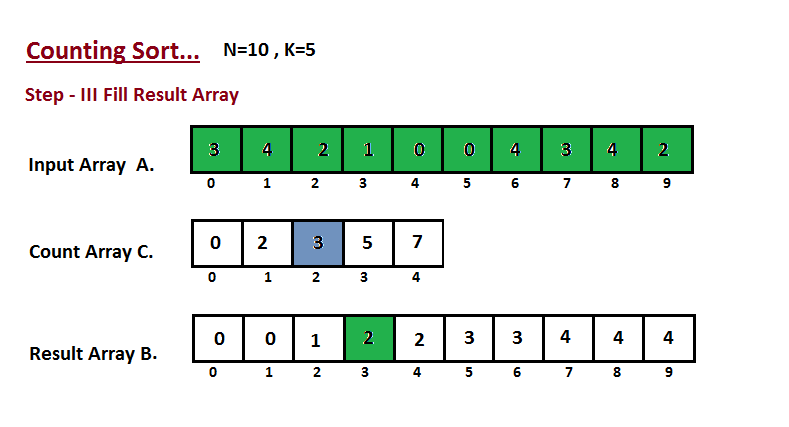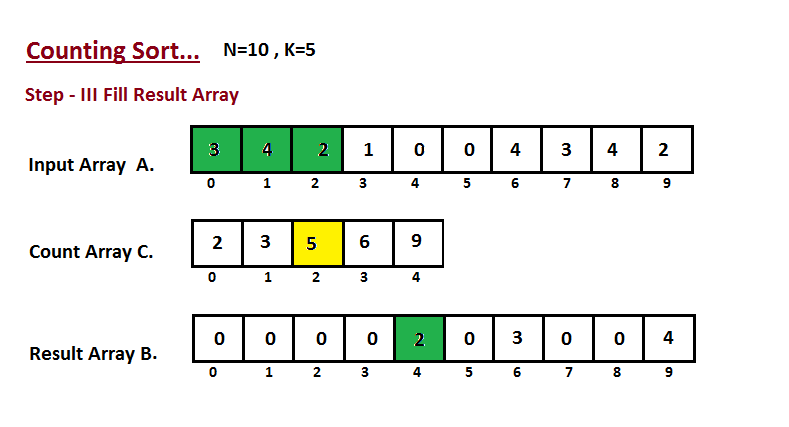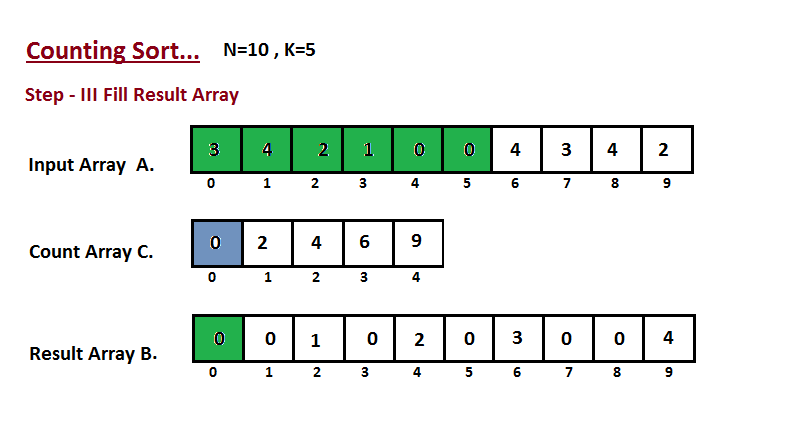
Thuật toán bố trí đếm trong C

Ví dụ minh họa

#include // Function that sort the given inputvoid counting_sort(int input<>, int n){ int output; // The đầu ra will have sorted đầu vào array int max = input<0>; int min = input<0>; int i; for(i = 1; i max) max = input; // Maximum value in array else if(input Kết quả:

Sorted Array : 1 1 2 3 4 4 5 5 7

Ví Dụ 2:

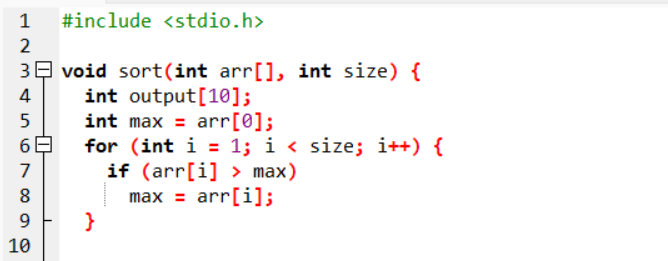
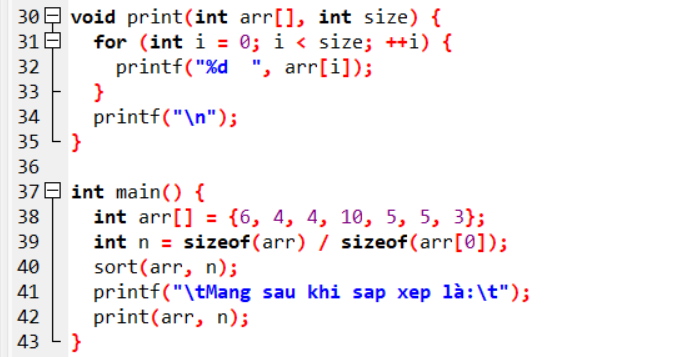
Hiển thị:

Thuật toán bố trí theo cơ số (Radix Sort)

Thuật toán sắp xếp cơ số là gì?

Sắp xếp dựa vào cơ số là 1 kỹ thuật sắp đến xếp những phần tử bằng cách nhóm các chữ số cô quạnh của một giá chỉ trị bao gồm cùng một vị trí. Sau đó, sắp xếp các thành phần theo sản phẩm tự tăng hoặc giảm.

Sắp xếp cơ số thường xuyên được dùng để làm sắp xếp số có rất nhiều chữ số (số lớn)

Giả sử, chúng ta có một mảng có 8 phần tử. Đầu tiên, chúng ta sẽ bố trí các thành phần dựa trên cực hiếm của vị trí đơn vị. Sau đó, họ sẽ sắp xếp các phần tử dựa trên cực hiếm của vị trí thứ mười. Quy trình này tiếp tục cho tới vị trí cuối cùng.

Giả sử, ta tất cả mảng ban sơ là <121,432,564,23,1,45,788>. Nó được sắp xếp theo cơ số như vào hình bên dưới.

Cách thức buổi giao lưu của thuật toán bố trí theo cơ số.

Bước 1: tìm thành phần lớn nhất trong mảng, được điện thoại tư vấn là trở nên max. Gọi X là số chữ số trong biến chuyển max. X hoàn toàn có thể tính toán được bỏi vì bọn họ phải đi qua tất cả các vị trí quan trọng của toàn bộ các phần tử. Trong mảng <121,432,564,23,1,45,788>, họ có số lớn nhất là 788. Nó gồm 3 chữ số. Vì chưng đó, vòng lặp sẽ lên đến chữ số hàng trăm.Bước 2: bây giờ, ta lần lượt trải qua từng địa chỉ quan trọng.

Sử dụng ngẫu nhiên kỹ thuật sắp xếp ổn định nào để sắp xếp những chữ số trên mỗi vị trí quan trọng. Bọn họ sử dụng sắp xếp đếm cho vấn đề này.

Sắp xếp các bộ phận dựa trên những chữ số hàng đơn vị (X=0)

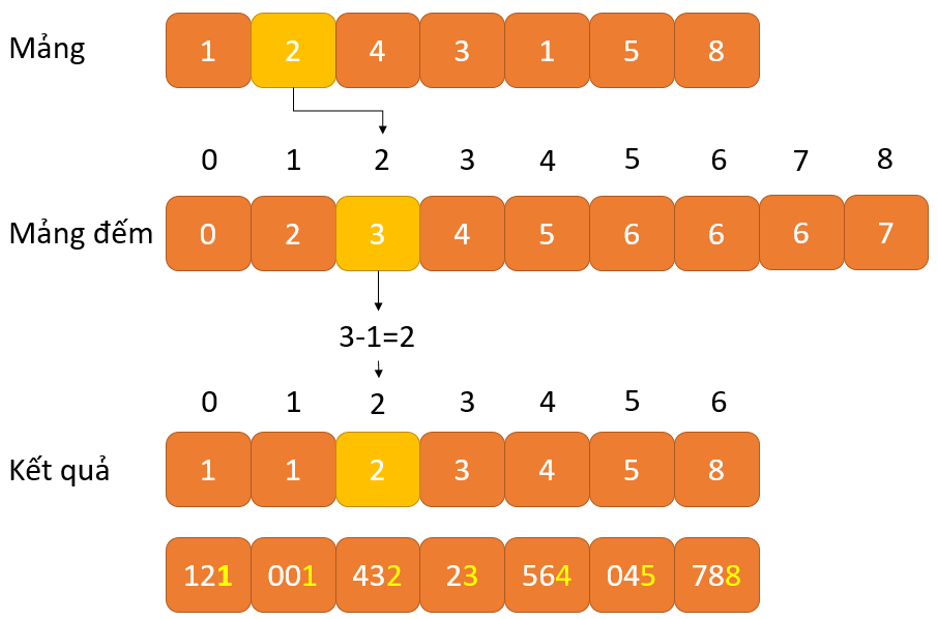
+ Sử dụng sắp xếp đếm để bố trí các phần tử dựa bên trên vị trí

Bước 3: Bây giờ, ta sẽ thu xếp các thành phần dựa trên những chữ số ở hàng chục.

Bước 4: Cuối cùng, sắp xếp các phần tử dựa trên các chữ số tại đoạn hàng trăm.

Sắp xếp cơ số trong C

Ví dụ minh họa

Hiển thị:

Thuật toán thu xếp theo khối (Bucket Sort)

Thuật toán thu xếp theo khối là gì?

Thuật toán sắp xếp dựa bên trên khối tốt Bucket Sort là 1 trong kỹ thuật sắp đến xếp các phần tử bằng phương pháp chia các phần tử thành một số nhóm được điện thoại tư vấn là khối xuất xắc Bucket ban đầu. Những phần tử bên trong mỗi nhóm được sắp tới xếp bằng cách sử dụng bất kỳ thuật toán sắp xếp cân xứng nào hoặc hotline đệ quy đến cùng một thuật toán.

Một số team được chế tạo ra. Mỗi nhóm cất đầy hàng loạt các thành phần nhất định. Các phần tử bên trong nhóm được sắp tới xếp bằng phương pháp sử dụng bất kỳ thuật toán làm sao khác. Cuối cùng, các thành phần trong khối được tập hợp lại để có được mảng bố trí theo thứ tự nhất định.

Quá trình thu xếp theo khối có thể được hiểu là 1 cách tiếp cận phân chia và tập hợp. Đầu tiên các thành phần được phân phân thành các nhóm kế tiếp các bộ phận của những nhóm được sắp đến xếp. Cuối cùng, các phần tử được tập thích hợp lại cùng với nhau với được thu xếp theo một lẻ tẻ tự.

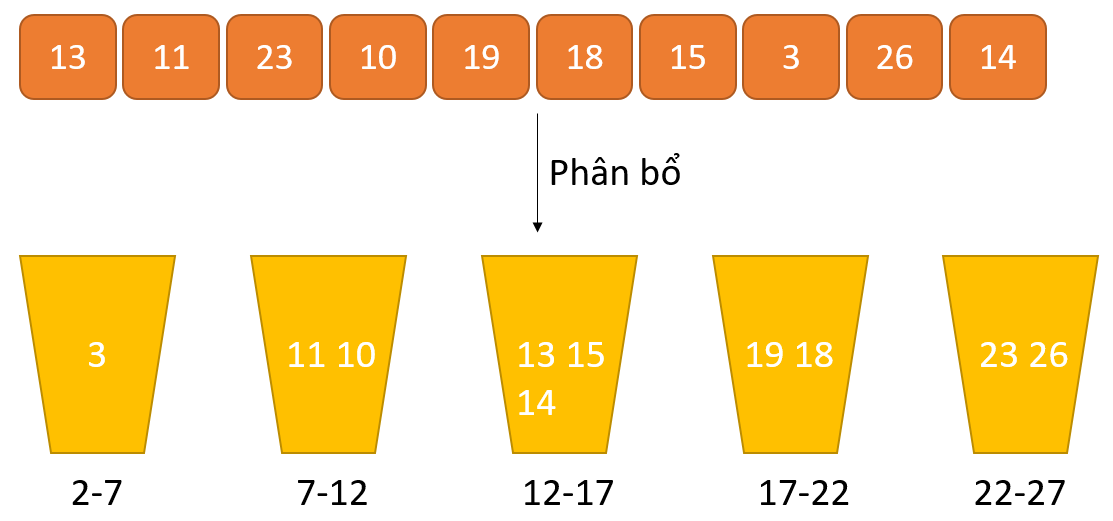
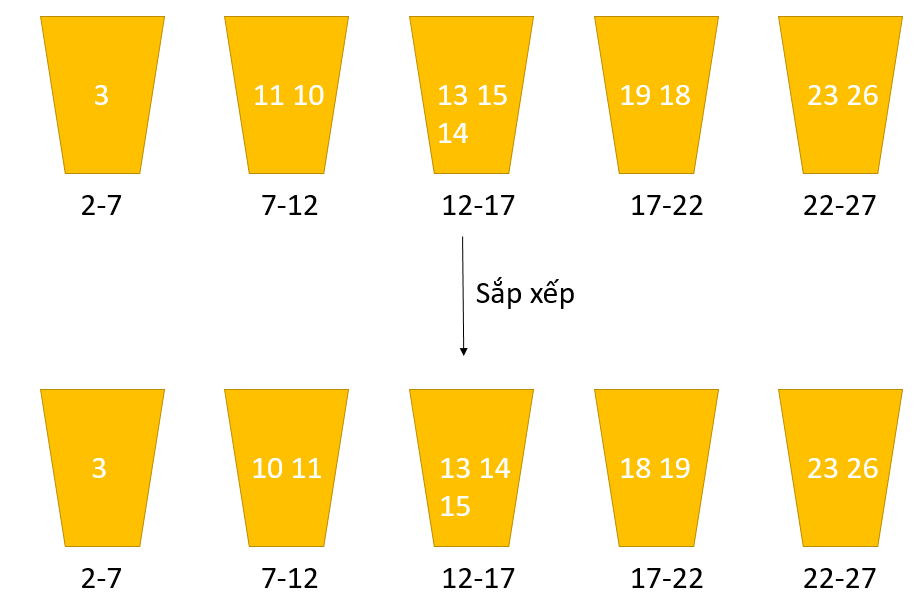
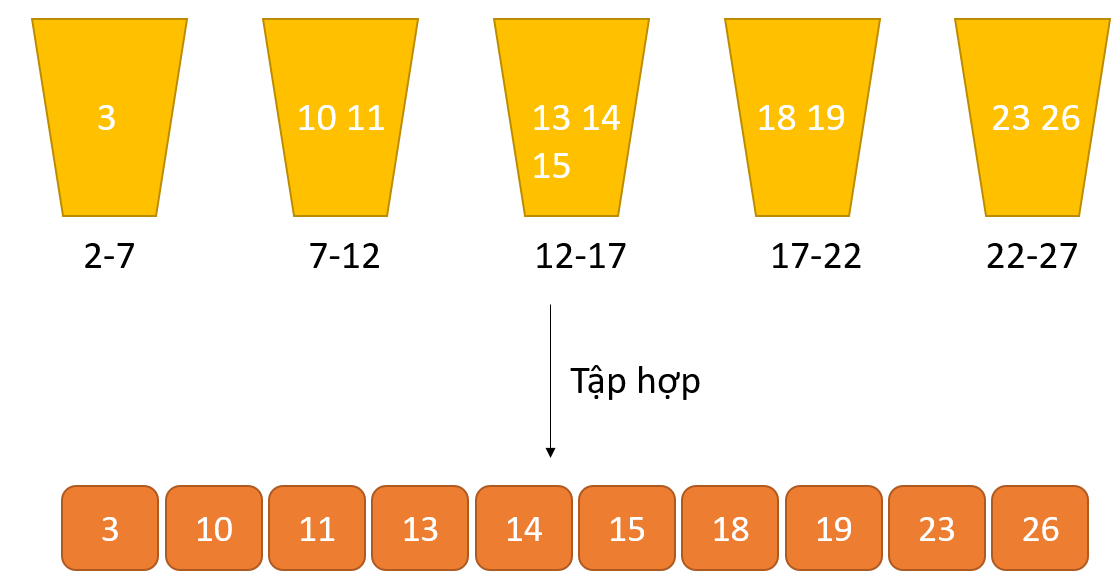
Sắp xếp theo khối với C

Ví dụ minh họa

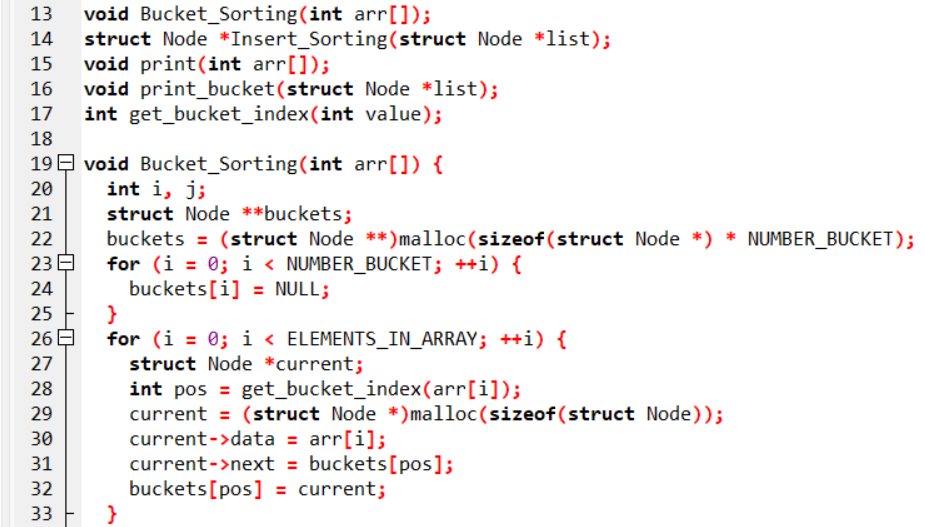
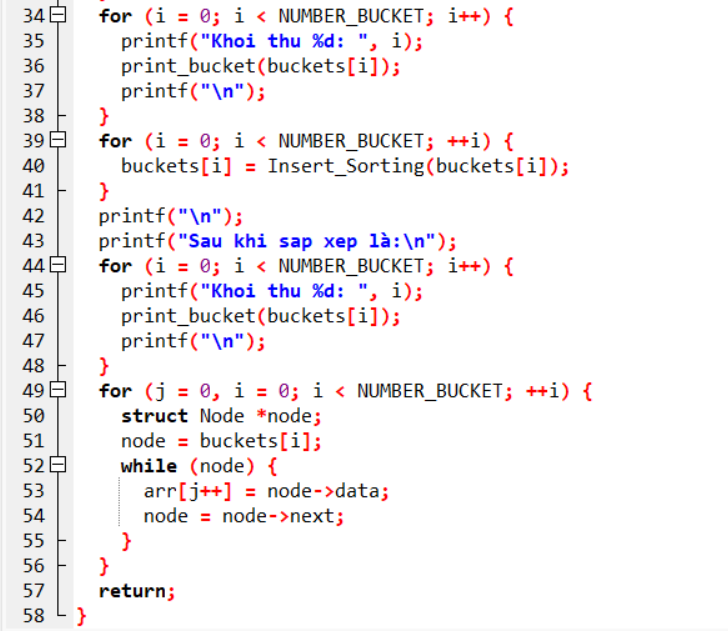
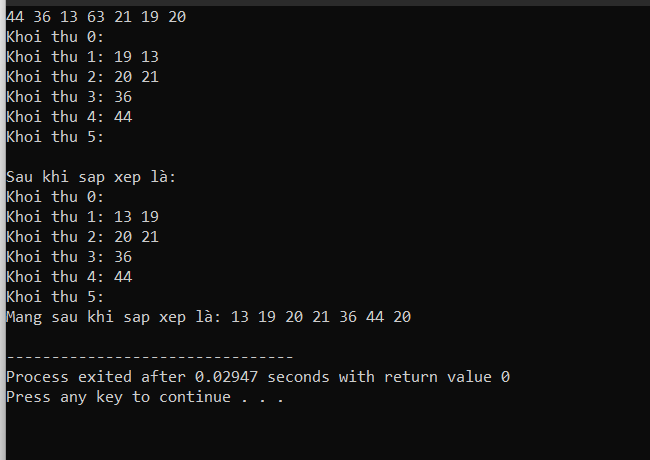
Thuật toán thu xếp vun đống (Heap Sort)

Thuật toán bố trí vun lô là gì?

Sắp xếp vun đụn hay Heap Sort là 1 trong những thuật toán chuẩn bị xếp phổ cập và công dụng trong lập trình. Học biện pháp viết thuật toán bố trí vun đống đòi hỏi kiến thức về nhị loại cấu trúc dữ liệu là mảng và cây.

Tập hợp số ban đầu mà chúng ta muốn thu xếp được lưu trữ trong một mảng, ví dụ, <12, 5, 78, 36, 25, 34> và sau khi sắp xếp, bọn họ nhận được một mảng đã thu xếp là <5, 12, 25, 34, 36, 78>

Sắp xếp vun đụn hoạt động bằng cách coi các bộ phận của mảng như một loại cây nhị phân trả chỉnh đặc trưng được call là Heap. Điều kiện tiên quyết là bạn phải biết về cấu tạo dữ liệu Heap và cây nhị phân hoàn chỉnh.

Mối dục tình giữa chỉ số của mảng và bộ phận của cây

Một cây nhị phân hoàn hảo có một công dụng mà chúng ta có thể sử dụng nhằm tìm nút nhỏ và nút phụ thân của ngẫu nhiên nút nào.

Nếu chỉ số của ngẫu nhiên phần tử làm sao trong mảng là i, phần tử trong chỉ số 2i+1 sẽ thay đổi nút nhỏ bên trái và thành phần trong chỉ số 2i+2 sẽ biến hóa nút con bên phải. Ngoài ra, nút cha của bất kỳ phần tử nào tại chỉ số i được cho bởi số lượng giới hạn dưới là (i-1)/2.

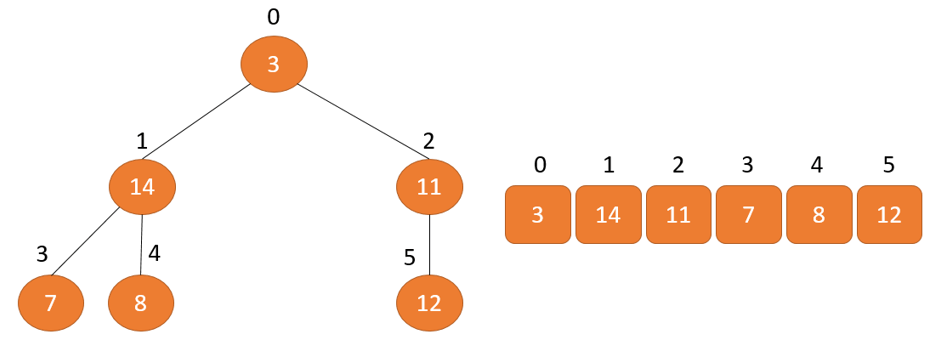
Nút bé bên trái của 3 (Chỉ số là 0)

= phần tử tại chỉ số (2*0+1)

= phần tử trong chỉ hàng đầu = 12

Nút con bên cần của 3

= thành phần tại chỉ số (2*0+2)

= bộ phận trong chỉ số 2 = 9

Tương tự,

Nút bé bên trái của 14 (Chỉ số 1)

= phần tử tại chỉ số (2*1+1)

= phần tử tại chỉ số 3 = 5

Nút bé bên đề nghị của 14

= thành phần tại chỉ số (2*1+2)

= thành phần tại chỉ số 4 = 6

Ta sẽ chứng thực rằng các quy tắc sẽ luôn luôn đúng cho việc tìm kiếm nút phụ thân của ngẫu nhiên nút nào

Nút cha của 11 (Vị trí 2)

= (2-1)/2 = 50% = 0.5 ~ chỉ số 0

= 3

Nút phụ vương của 14 (Vị trí 1)

= (1-1)/2 = chỉ số 0

= 3

Hiểu được câu hỏi ánh xạ của các chỉ số của mảng với các vị trí trong cây là rất đặc biệt để đọc được giải pháp thức hoạt động vui chơi của cấu trúc tài liệu Heap và bí quyết nó được sử dụng để thực hiện sắp xếp vun đống.

Cấu trúc dữ liệu Heap là gì?

Heap là một cấu trúc dữ liệu đặc trưng dựa trên cấu tạo cây. Cây nhị phân được hiểu tuân theo cấu trúc dữ liệu đống nếu

Nó là một trong cây nhị phân trả chỉnh.

Tất cả các nút vào cây tuân theo nằm trong tính nhưng chúng béo hơn phần tử con của chúng, tức là thành phần lớn nhất nằm ở vị trí nút nơi bắt đầu và các bộ phận con của nó nhỏ tuổi hơn nút gốc,…. Một Heap bởi vậy được call là Max heap. Nếu nắm vào đó, tất cả các nút đều nhỏ dại hơn nút bé của chúng, nó được điện thoại tư vấn là Min Heap.

Hình dưới đây sẽ minh họa về kết cấu dữ liệu Max Heap và Min Heap.

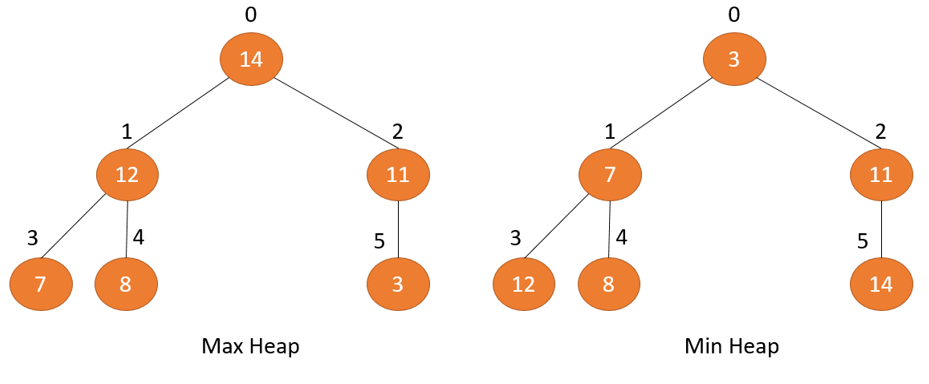
Làm cố gắng nào nhằm để tạo một kết cấu Heap cho 1 cây?

Bắt đầu xuất phát từ 1 cây nhị phân trả chỉnh, chúng ta cũng có thể sửa thay đổi nó để vươn lên là Max Heap bằng phương pháp thực hiện tại một hàm mang tên là Heapify trên toàn bộ các bộ phận không nên là nút lá của Heap. Bởi hàm Heapify áp dụng đệ quy nên hoàn toàn có thể khó vắt bắt. Vì chưng vậy, trước tiên họ hãy nghĩ về cách ta sẽ tạo nên Heap cho 1 cây chỉ với bố phần tử.

heapify(array)

Root = array<0>

Largest = largest( array<0> , array <2*0 + 1>. Array<2*0+2>)

if(Root != Largest)

Swap(Root, Largest)

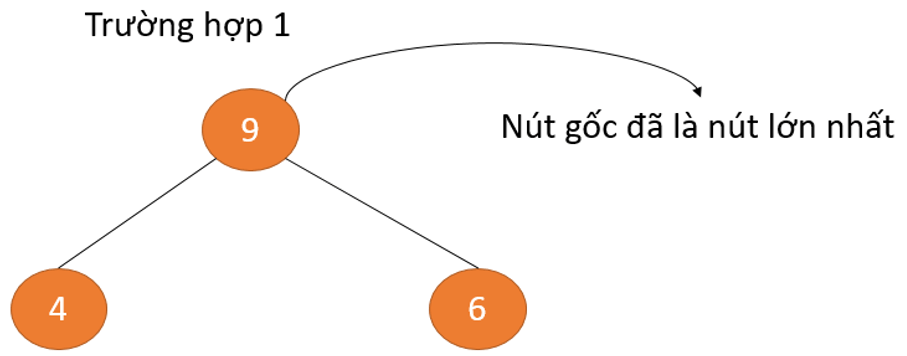
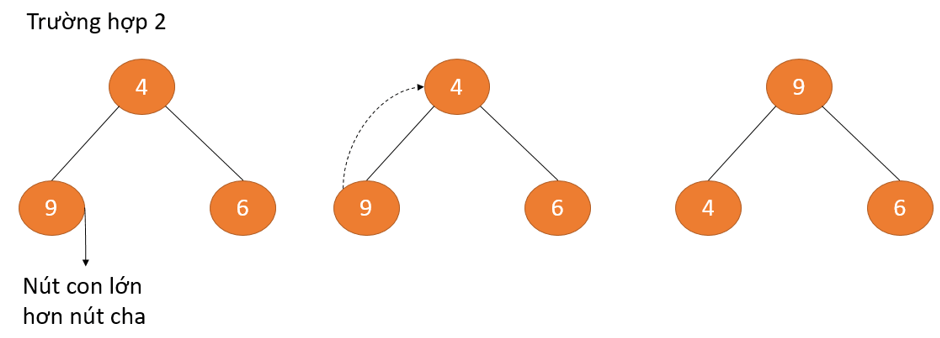
Ví dụ trên giới thiệu 2 ngôi trường hợp, một trong các đó tất cả nút cội là bộ phận lớn duy nhất và chúng ta không đề nghị phải làm cái gi cả. Và 1 phần tử khác trong các số ấy nút gốc bao gồm một nút con to hơn và bọn họ cần hoán đổi để gia hạn thuộc tính Max Heap.

Nếu ta đã thao tác làm việc với các thuật toán đệ quy, ta rất có thể đã xác minh rằng đây đề xuất là trường hợp đại lý (trường đúng theo để xong xuôi lời điện thoại tư vấn đệ quy).

Ví dụ 2:

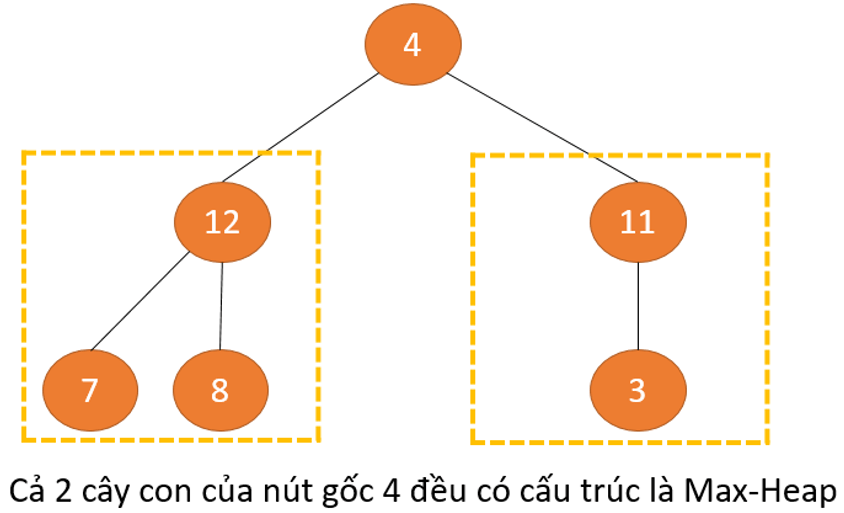
Tuy nhiên, nút trên cùng không hẳn có cấu trúc Max Heap nhưng toàn bộ các cây nhỏ đều là Max Heap.

Để duy trì thuộc tính Max Heap cho toàn bộ cây, bọn họ sẽ phải liên tiếp đẩy 2 cây xuống dưới cho tới khi nó đến đúng vị trí của nó.

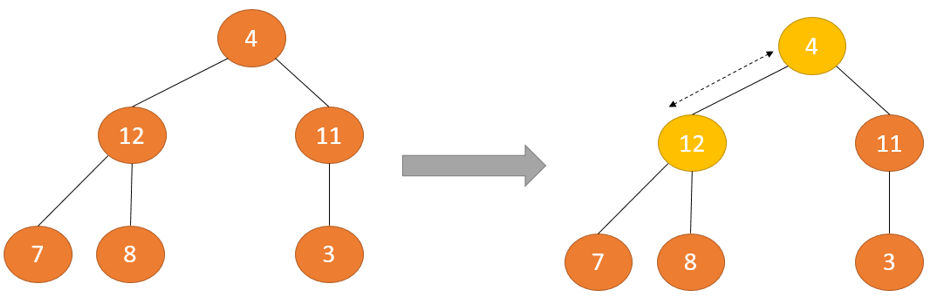
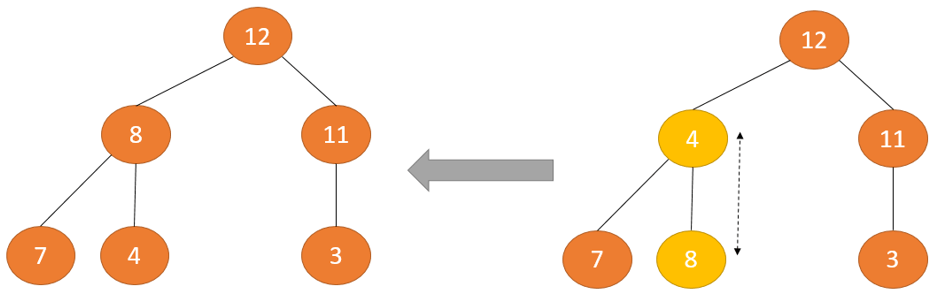
Do đó, để bảo trì thuộc tính Max Heap vào một cây nhưng mà cả hai cây bé đều là Max Heap, họ cần thực hiện quá trình Heapify trên nút gốc nhiều lần cho tới khi nó to hơn cây nhỏ của nó hoặc nó biến chuyển một nút lá.

Chúng ta rất có thể kết đúng theo cả hai đk này vào một hàm Heapify như sau:

void heapify(int arr<>, int n, int i) int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left arr)largest = left;if (right arr)largest = right;if (largest != i) swap(&arr, &arr);heapify(arr, n, largest);Hàm này vận động hiệu quả mang lại trường hợp các đại lý và cho 1 cây có kích cỡ bất kỳ. Bởi vì đó, bạn có thể di chuyển nút gốc mang đến vị trí đúng chuẩn để gia hạn trạng thái Max Heap cho ngẫu nhiên kích thước cây làm sao miễn là các cây nhỏ có kết cấu Max Heap.

Xây dựng cấu tạo Max heap

Để chế tác Max Heap từ bất kỳ cây nào, ta có thể bắt đầu xếp từng cây con từ dưới lên và có được kết cấu Max Heap sau khoản thời gian hàm được áp dụng cho toàn bộ các phần tử bao hàm cả phần tử gốc.

Trong trường đúng theo của một cây hoàn chỉnh, chỉ số đầu tiên của một nút chưa hẳn nút lá được cho vì chưng n/2-1. Tất cả các nút khác kế tiếp là nút lá và vì đó không cần phải tạo cấu tạo heap mang lại nó nữa.

Vì vậy, bạn có thể xây dựng một cấu trúc Max heap như sau:

for (int i = n / 2 - 1; i >= 0; i--)

heapify(arr, n, i);

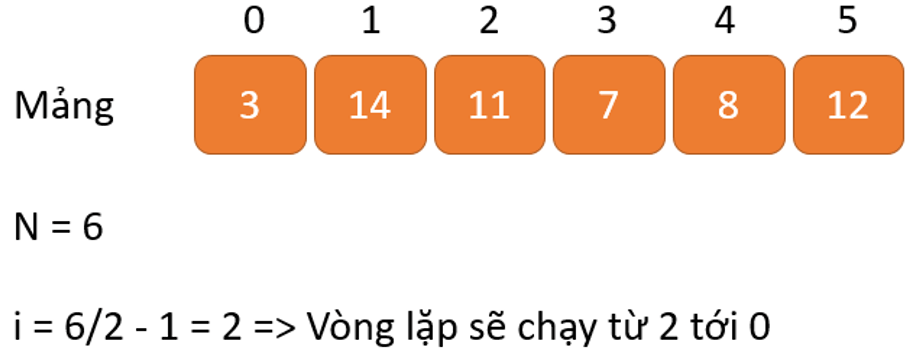
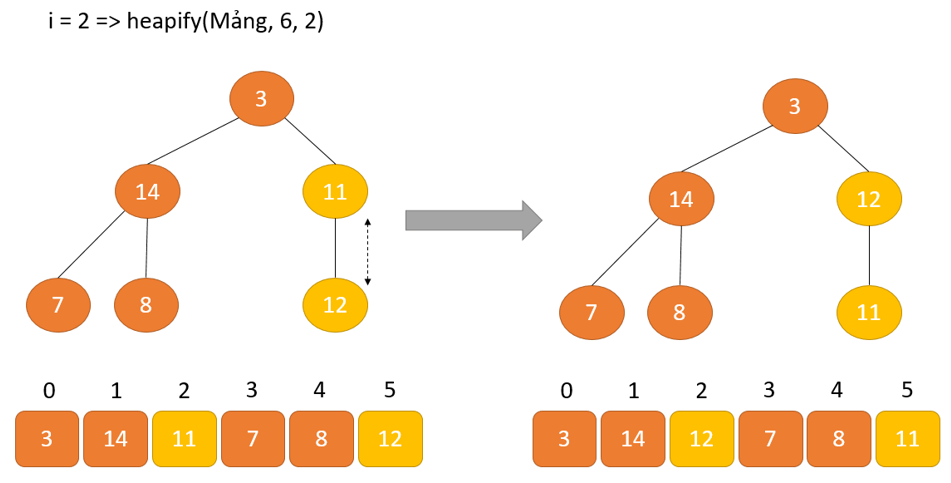
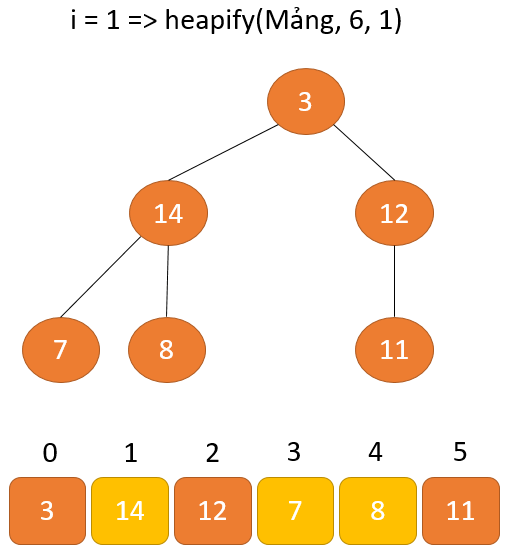
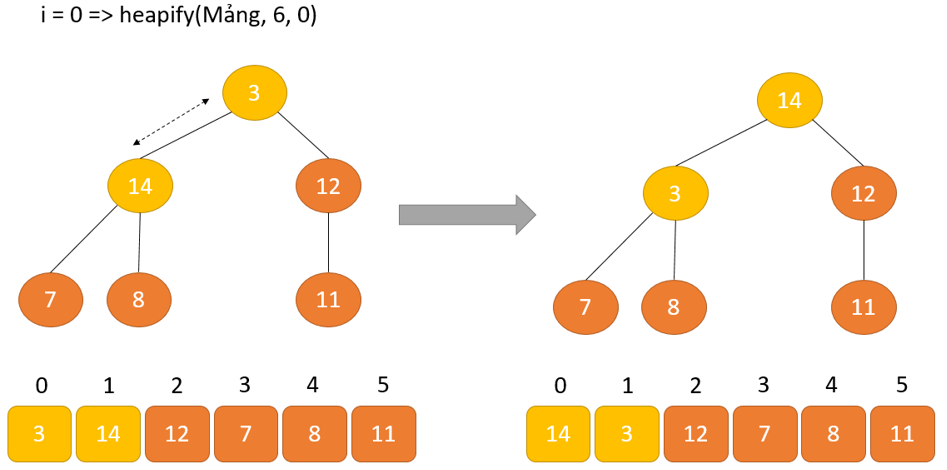
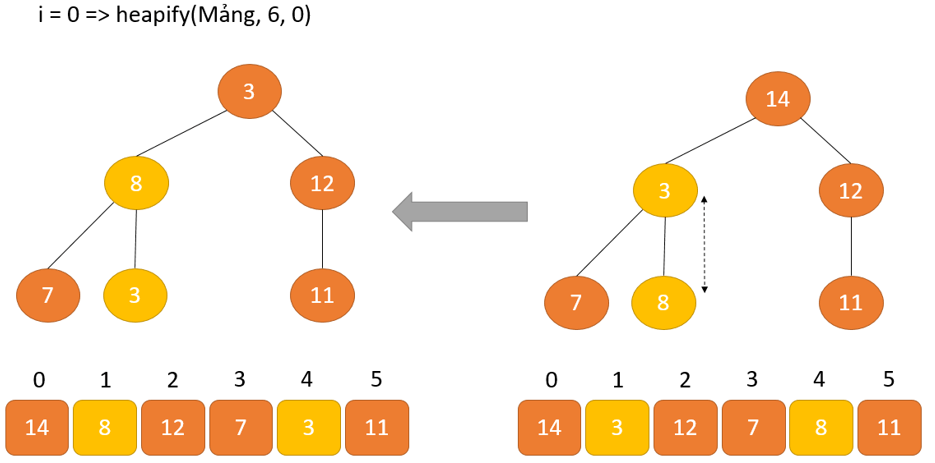
Như diễn đạt trong sơ vật trên, chúng ta sẽ bước đầu bằng biện pháp xếp vun đống cho những cây bé dại nhất thấp độc nhất vô nhị và dần dần di gửi lên cho đến khi chúng ta đạt đến bộ phận gốc.

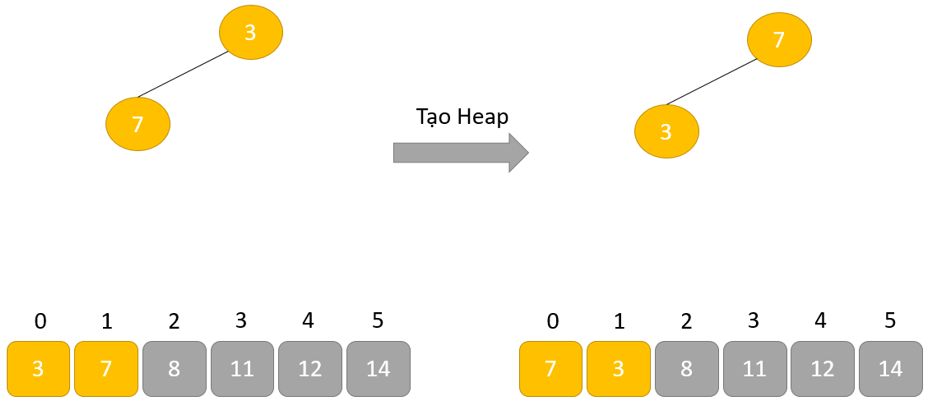
Sắp xếp vun đống vận động như nào?

Vì cây thỏa mãn nhu cầu thuộc tính Max Heap, nên thành phần lớn tuyệt nhất được lưu trữ tại nút gốc.

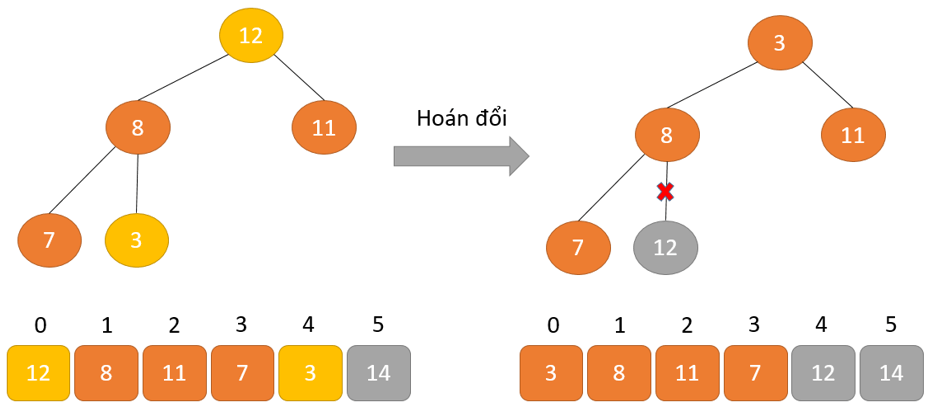
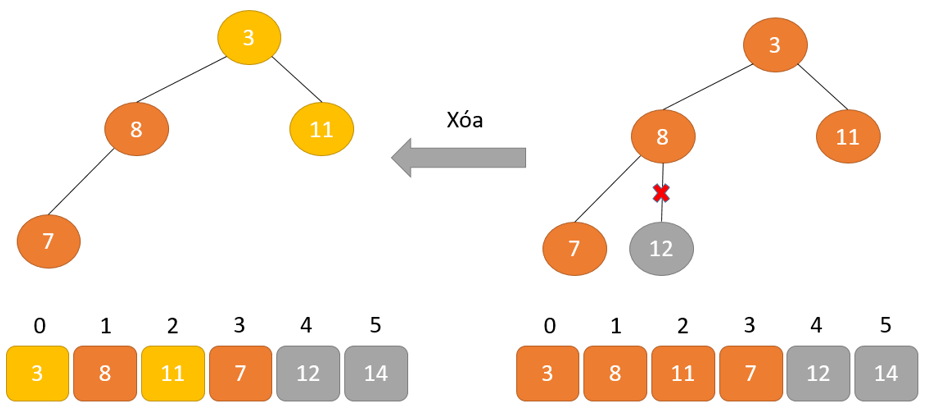
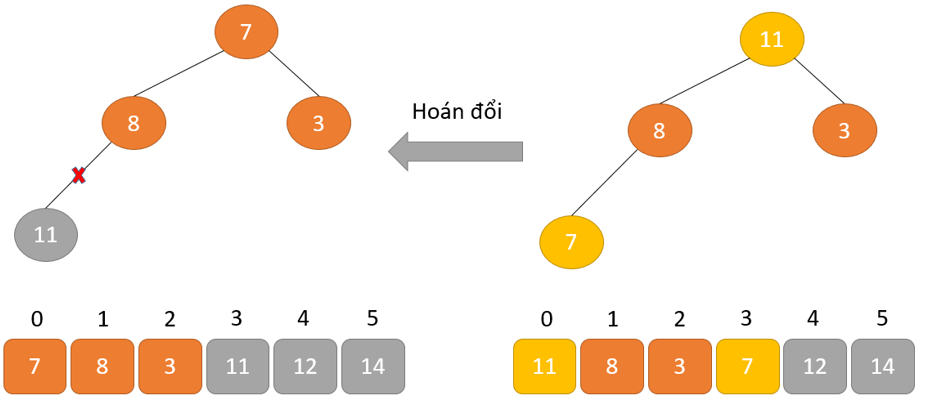
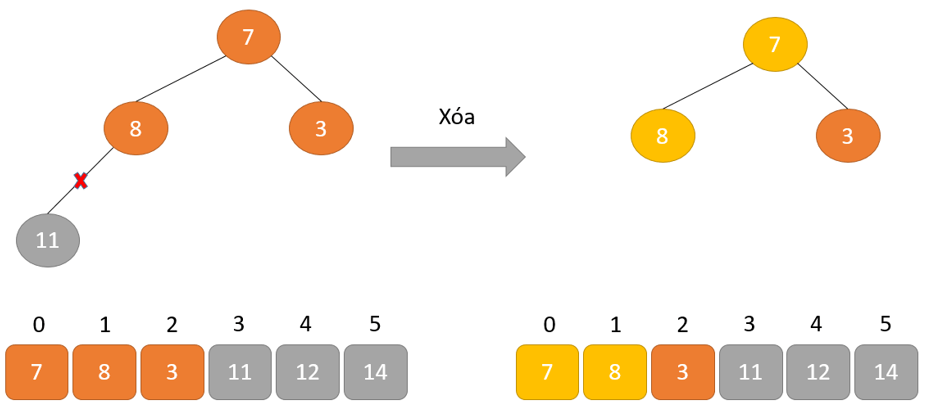
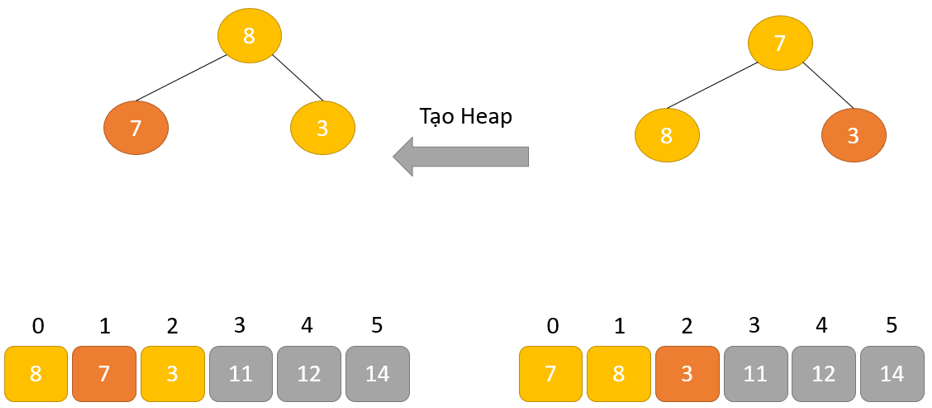
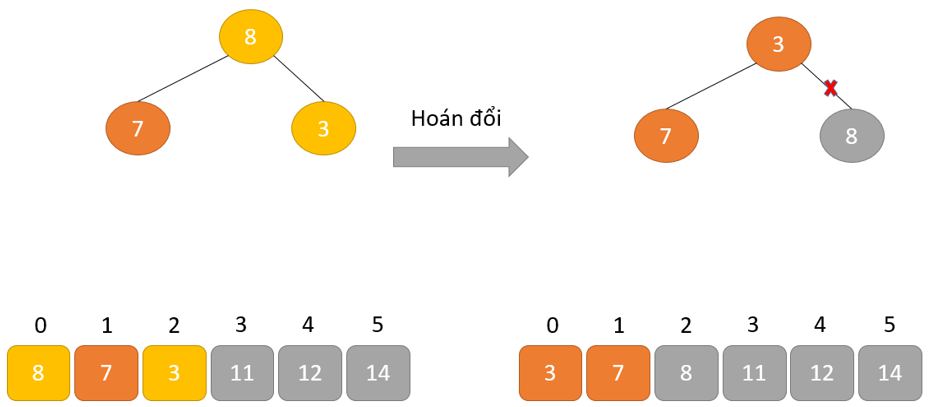
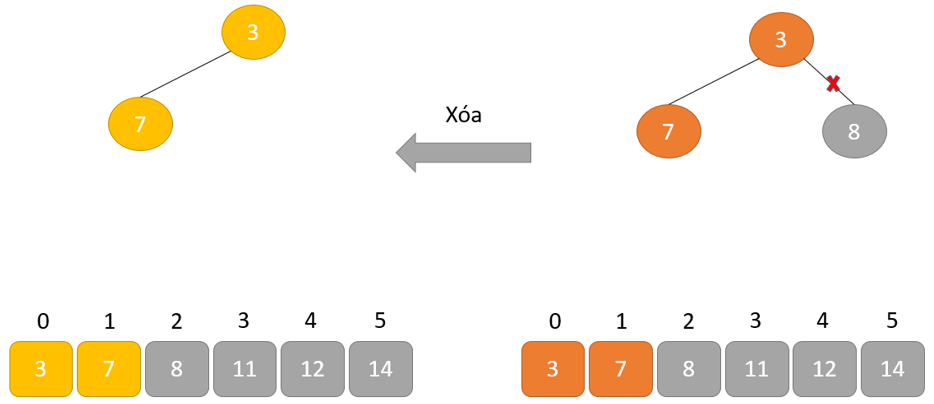
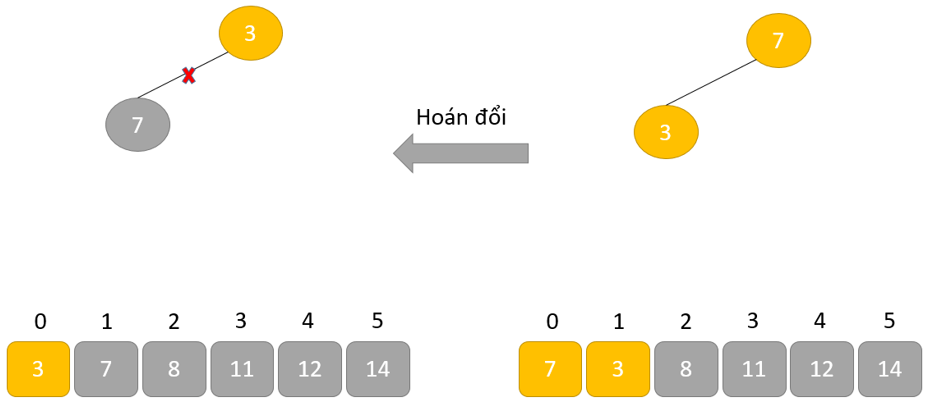
Hoán đổi: loại bỏ phần tử gốc và đặt tại cuối mảng (vị trí thiết bị n). Đặt thành phần cuối thuộc của cây (đống) vào địa điểm trống.

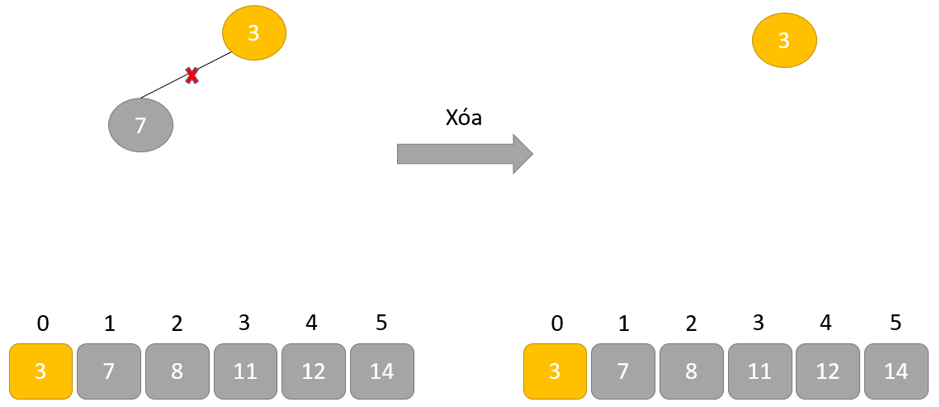
Xóa: Giảm kích cỡ của Heap đi 1 solo vị.

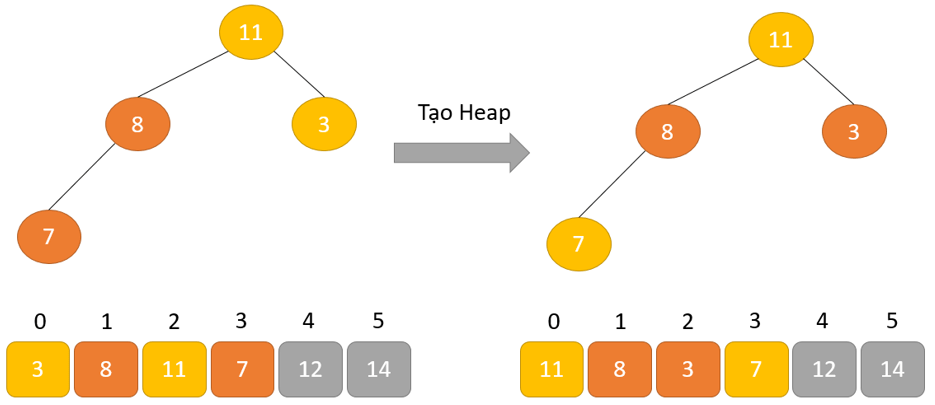
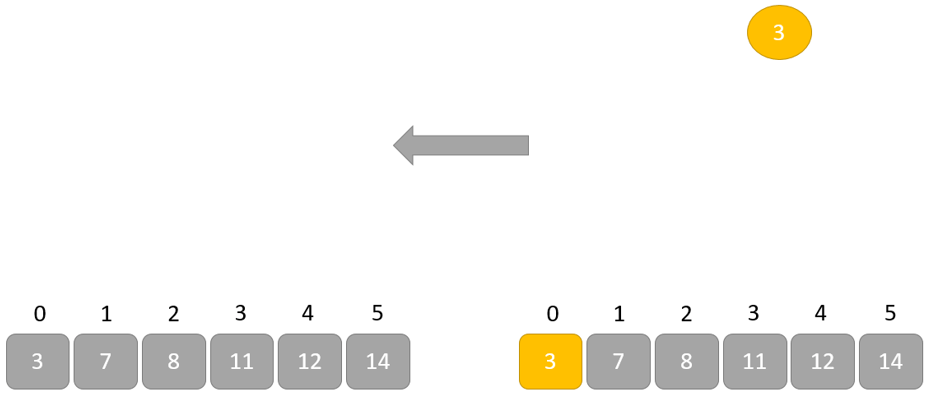
Heapify: Tạo kết cấu Heap cho bộ phận gốc để chúng ta có thành phần cao tốt nhất ở nút gốc.

Quá trình này được lặp lại cho đến khi tất cả các bộ phận của danh sách được sắp xếp.

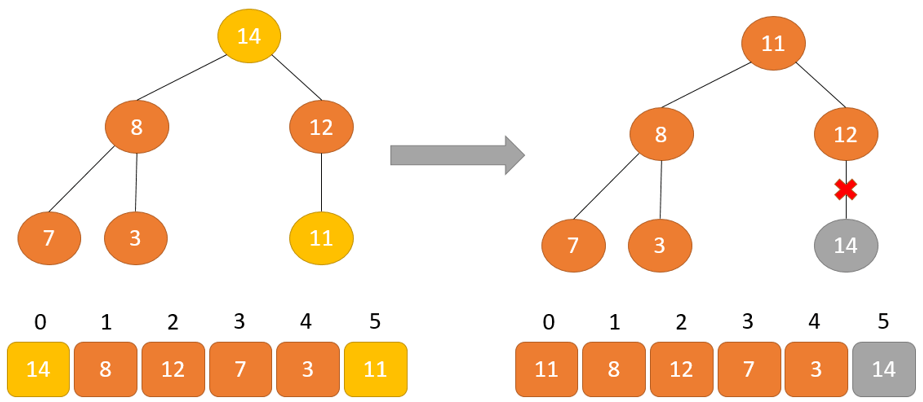
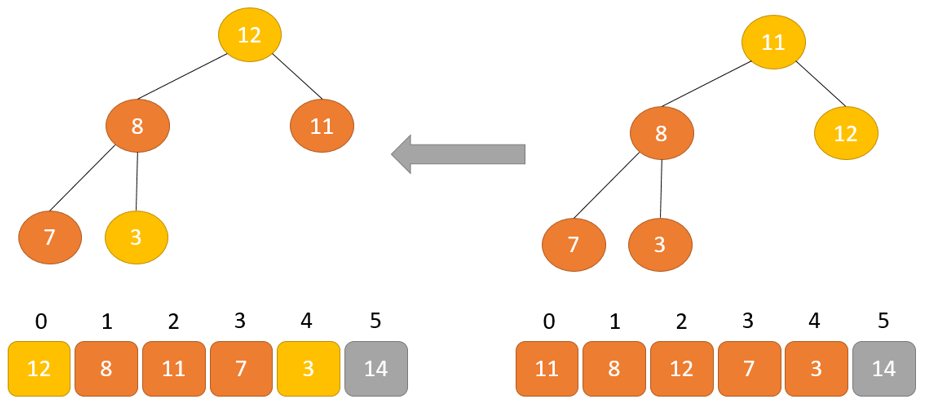
Sắp xếp vun gò với C

Ví dụ minh họa

for (int i = n - 1; i >= 0; i--) swap(&arr<0>, &arr);//Tạo kết cấu heap cho thành phần gốc để lấy ra thành phần lớn nhấtheapify(arr, i, 0);#include void swap(int *a, int *b) int c = *a;*a = *b;*b = c;void heapify(int arr<>, int n, int i) int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left arr)largest = left;if (right arr)largest = right;if (largest != i) swap(&arr, &arr);heapify(arr, n, largest);void sort_heap(int arr<>, int n) for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);for (int i = n - 1; i >= 0; i--) swap(&arr<0>, &arr);heapify(arr, i, 0);void print(int arr<>, int n) {for (int i = 0; i Kết quả:

Mảng sau khoản thời gian sắp xếp là:

3 7 8 11 12 14

Lời kết

Có không ít loại thuật toán sắp đến xếp, trong bài bác này tôi chỉ nêu ra một số phương pháp thường áp dụng nhất và ứng dụng chúng với ngôn ngữ C. Yêu cầu nhớ các thuật toán hoàn toàn có thể áp dụng với bất kì ngôn từ nào, chỉ với cách xúc tiến chúng trong mỗi ngôn ngữ sẽ hơi khác nhau mà thôi

Sắp xếp là 1 giữa những thuật toán bom tấn và quan trọng trong lập trình. Vậy đâu là thuật toán chuẩn bị xếp xuất sắc nhất? Hãy cùng khám phá nhé

Tại sao rất cần phải sắp xếp?

Thử tượng tượng bạn phải tra cứu 1 từ trong từ điển, tuy vậy cuốn từ bỏ điển đó lại không được sắp xếp theo sản phẩm công nghệ tự alphabet, các từ trong từ điển được bố trí theo 1 quy luật ngẫu nhiên. Khi đó, việc bạn buộc phải làm là lật từng trang, với từng trang chúng ta lại yêu cầu cố tìm kiếm coi từ bạn phải tìm có trong trang đó hay không. Và vấn đề này khiến cho bạn đề nghị bỏ ra khá nhiều thời gian và công sức. Tuy nhiên, với 1 cuốn tự điển được bố trí theo máy tự alphabet thì các bước tra cứu của bạn là khá dễ dàng dàng.

(link ảnh:Dictionary.com chooses its Word of the Year for 2011 - pr Daily (google.com))

Hay thử mang 1 lấy ví dụ khác, nếu như khách hàng được cho một danh sách điểm của sinh viên toàn trường, yêu thương cầu đặt ra là tìm kiếm sinh viên tất cả điểm số cao nhất, lúc ấy việc chúng ta phải có tác dụng là cẩn thận qua từng sinh viên và tìm ra sinh viên bao gồm điểm số cao nhất, công việc này khá dễ dãi và hoàn toàn hoàn toàn có thể thực hiện tại được, tuy nhiên câu chuyện không dừng lại ở đó. Bởi nếu công việc yêu ước là lọc ra đứng top 10 sinh viên bao gồm điểm số cao nhất để ship hàng công tác khen thưởng, với một danh sách không được sắp xếp bạn sẽ phải lần lượt tìm ra sinh viên tất cả điểm số cao trang bị nhất, lắp thêm 2, máy 3, ... Việc này cũng làm cho mình tốn tương đối nhiều thời gian cùng công sức, quan trọng khi con số sinh viên trong danh sách càng tăng thì thời gian và công sức bạn bỏ ra cũng tỉ lệ thuận theo số lượng đó. Tuy nhiên với một danh sách sinh viên cùng với điểm số đã được sắp xếp(giả sử bố trí theo thiết bị tự bớt dần), thì công việc của bạn dễ dàng và đơn giản là lấy ra 10 sinh viên thứ nhất trong danh sách. Qua số đông ví dụ trên hoàn toàn có thể thấy rằng, sắp tới xếp làm cho những thao tác tìm kiếm tuyệt lọc của họ trở nên thuận tiện hơn cực kỳ nhiều. Cũng chính vì vậy, bố trí là một trong những bài toán đặc biệt quan trọng trong lập trình. Vào lập trình hiện tại có không dưới 20 thuật toán ship hàng cho các bước sắp xếp.

	Độ phức tạp
STT	Thuật toán	Tốt nhất	Trung bình	Xấu nhất	Bộ nhớ	Stable
1	Bubble Sort	O(n)	O(n²)	O(n²)	O(1)	Có
2	Shaker Sort	O(n)	O(n²)	O(n²)	O(1)	Có
3	Selection Sort	O(n²)	O(n²)	O(n²)	O(1)	Không
4	Insertion Sort	O(n)	O(n²)	O(n²)	O(1)	Có
5	Binary Insertion Sort	O(n)	O(n²)	O(n²)	O(1)	Có
6	Shell Sort	O(nlogn)	depends on gap sequence	O(n2)	O(1)	Không
7	Heap Sort	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	Không
8	Merge Sort	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	Có
9	Quick Sort	O(nlogn)	O(nlogn)	O(n²)	O(logn)	Có/Không
10	Counting Sort	O(n+k)	O(n + k)	O(n + k)	O(n + k)	Có
11	Radix Sort	O(kn)	O(nk)	O(nk)	O(n + k)	Có
12	Flash Sort	O(n)	O(n + r)	O(n²)	O(m)	Không

Bảng thống kê một số thông số của những thuật toán(Theo Wikipedia)

Đâu bắt đầu là thuật toán sắp đến xếp tốt nhất?

Có lẽ đó cũng là thắc mắc của không hề ít người khi bắt đầu học lập trình, trong nội dung bài viết nay hãy cùng mình thực hiện một thử nghiệm nhỏ dại với 12 thuật toán bố trí để đưa ra câu vấn đáp nhé! thử nghiệm được tiến hành với form size dữ liệu đầu vào lần lượt là 3.000, 10.000, 100.000, 300.000, với những loại tài liệu lần lượt là mảng gồm thứ tự ngẫu nhiên, mảng bao gồm thứ từ tăng dần, mảng gồm thứ tự sút dần, mảng gần như đã bao gồm thứ từ tăng dần(sai ở một số vị trí), và mục đích là đem đến mảng bao gồm thứ từ bỏ tăng dần. Toàn thể source code các chúng ta có thể tham khảo nghỉ ngơi đây: Hai
Duc0147/sorting
Algorithm (github.com)

Cấu hình máy tiến hành thử nghiệm:

CPU: Intel(R) Core(TM) i5 4200U CPU
1.6GHz 2.3 GHz.RAM: 4 GB DDR3L 1600MHz bus.Hệ quản lý và điều hành Windows 10 Pro.Compiler: Visual Studio 2015.

Xem thêm: Chat Với Người Nước Ngoài Ở Việt Nam, Top 13+ Ứng Dụng Chat Với Người Nước Ngoài 2023

Bảng những thống kê với dữ liệu đầu vào ngẫu nhiên

Bảng thống kê với tài liệu đầu vào tất cả thứ từ bỏ tăng dần

Bảng thống kê với tài liệu đầu vào gồm thứ tự bớt dần

Bảng thống kê với tài liệu đầu vào gần như là có trang bị tự tăng dần

Nhận xét:

Với kích cỡ dữ liệu nguồn vào nhỏ(3000) chú ý chung vận tốc chênh lệch của các thuật toán là ko rõ để thừa nhận thấy.Với mảng sẽ được sắp xếp, thì Bubble Sort và Shaker Sort đến tốc độ sớm nhất có thể do ngân sách để biết được đây là mảng bao gồm thứ từ bỏ của 2 thuật toán bên trên là O(n).Với mảng gần như là đã được thu xếp thì Insertion Sort với Binary Insertion Sort là hầu như sự lựa chọn cực tốt do số phép hoán đổi phải thực hiện ít.Selection Sort mang đến tốc độ muộn hơn trong phần lớn trường hợp bởi độ phức tạp luôn luôn là O(n2), cho nên Selection Sort chỉ nên dùng cho các trường hợp số lượng thành phần cần sắp đến xếp không thật nhiều.Với mảng gần như là đã được thu xếp thì Shaker Sort cho vận tốc nhanh hơn đáng kể so với Bubble Sort, vì thu không lớn được khoảng chừng phải săn sóc tiếp theo sau khoản thời gian duyệt.Shell Sort, Heap Sort, Merge Sort với Quick Sort có vận tốc ổn định xuyên thấu cả 4 loại dữ liệu đầu vào.Flash Sort(được phát minh bởi Karl-Dietrich Neubert vào khoảng thời gian 1998) là 1 trong thuật toán cho tốc độ nhanh(thậm chí nhanh hơn hết Quick Sort) và tiêu tốn rất ít bộ nhớ, mặc dù nhiên phương pháp xây dựng thuật toán trên khá phức hợp mà nếu tất cả dịp mình sẽ sở hữu một bài viết riêng để nói tới thuật toán này.Counting Sort với Radix Sort là đa số thuật toán cho tốc độ nhanh, tuy nhiên cần tấn công đổi bằng phương pháp sử dụng thêm cỗ nhớ.

Kết luận

Qua gần như thống kê với nhận xét sinh sống trên, mình mong muốn các bạn đã có cho bạn dạng thân câu trả lời "Đâu bắt đầu là thuật toán sắp xếp giỏi nhất?". Còn với bản thân câu trả lời đó là: không có thuật toán sắp xếp nào là xuất sắc nhất, nó chỉ là đơn giản và dễ dàng là sự tiến công đổi thân không gian, thời gian và công sức bỏ ra để xây cất thuật toán, cũng chính vì vậy tùy thuộc vào từng loại dữ liệu đầu vào, không gian bộ nhớ lưu trữ cho phép, tốc độ cần thực thi, cấu hình máy thực hiện thuật toán mà gạn lọc thuật toán mang lại phù hợp. Hẹn chạm mặt lại các bạn trong các bài viết tiếp theo!